
Security as a top priority.
Some people take private key security very seriously. After all if you lose your private key through theft, fire, or a tragic boating accident, the money is gone forever. That's a pretty heavy risk in terms of storing significant wealth by oneself. Nobody said being your own bank was easy.
Of course there's also a big difference between something like Hive and Bitcoin. On Hive if your active key gets stolen you can just change it with the owner key. Even if the owner key is compromised it can be reset with the recovery feature. Meanwhile, a network like Bitcoin (and pretty much everything else) is far less forgiving.
No such thing as true random
To those who don't know better, producing a random number seems like a very trivial task, but it is actually quite a complicated topic, especially in world of computing. Algorithms can be created that will output a seemingly random dataset if one does not have access to the inputs. However, with access to the inputs these algorithms can always be reverse-engineered to divine future outputs. This is a critical attack vector against digital entropy.
What is entropy?
Entropy is a scientific concept that is most commonly associated with a state of disorder, randomness, or uncertainty.
It should come as no surprise that crypto private keys need to be as random as possible to avoid being reverse engineered by bad actors. But how does one accomplish such a feat? Do we simply trust a hardware wallet that comes in the mail and hope for the best?
Many crypto users do just that without giving it a second thought, and to be fair that likely ends up being a viable strategy for most, but there are those out there who are much too paranoid to simply trust multiple third parties in this fashion (hardware wallet provider and logistics service). So they come up with the most old-school analog way of going about creating private key entropy.
https://docs.google.com/spreadsheets/d/1zEDR4O6jrRF_xCbmdMomHnNIBVpTeqtgThhFOjB-1ws/edit#gid=0
Upon seeing this Tweet I immediately asked for a link to the spreadsheet and was pretty happy to gain access to it. Hopefully the link above stays active for a while and anyone with an interest in this topic can copy it to their own drive.
Every word in a seed has 11 bits
Why 11 bits? It is pretty random, is it not? Why not 12 bits? That would be the same as 3 hexadecimal characters. Why not just round up to 16 bits for a standard 2 bytes of data?
Turns out the reason for doing it this way is that we require 128 bits of entropy with 4 bits for checksum on a 12-word key.
https://bitcoin.stackexchange.com/questions/88689/are-checksums-included-in-mnemonic-seed-phrases
The way that BIP 39 makes the mnemonic is by generating some initial entropy that is n bits in length. The checksum is then the first n / 32 bits of the SHA256 hash of the entropy. This is just concatenated to the end of the entropy. The mnemonic is then encoded by dividing the entropy into groups of 11 bits and using the resulting 11 bit number as an index into a list of 2048 words.
11 bits per word * 12 words = 132 bits total
This is actually something that I always wondered about but never actually figured out until just now. I don't know if you guys have done this, but I've tried to type in random seeds into Metamask just to see if it would create a random wallet way back in 2018. Most of the wallets I tried to create would not work and threw an error, but every once and a while it would work and I had no idea why. Now I know.
Checksum!
The reason for this behavior is that the last word of every seed phrase contains information about the previous words. Therefore if we just pick a last word randomly it's going to throw an error unless we just happen to randomly guess correctly.
For a twelve-word seed guessing correctly would be relatively easy because there are only 4 bits of checksum, meaning that there's a 1/16 chance of guessing correctly and a 15/16 chance of failure. However with a 24 word seed there are 8 checksum bits which means that guessing correctly by accident would only have a 1/256 chance. Good to know!

Are you lost yet?
I'm guessing that at least half of my readers have no idea what I'm talking about, but that's okay you are not alone. Hopefully after I finish this post off with the tutorial of how to actually apply this knowledge it will make a little bit more sense.
Tutorial: Creating a 12-word seed with dice rolls.
Requirements:
- Three D8 dice and a single D4 die.
- Twelve rolls.
- Access or ability to convert binary entropy to hex.
- Access to SHA-256 algorithm that can process hex numbers (not strings).
- Ability to convert a valid seed into an actual crypto wallet (pubkey at minimum).
Because this seed is fake I'll just use Google RNG and a handful of other online tools, but for anyone doing this to capitalize on real offline security all these things need to be available offline using actual dice and a device that can't connect to the Internet (ever).
Many will also inevitably wonder if a 24-word seed is more secure than a 12-word seed. Unfortunately, it is not because Bitcoin uses 128 bit encryption (sort of). I've seen many discussions take place among people who know a lot more than me about cryptography and ultimately the consensus concludes that 24-words is unnecessary for most applications thus far, including Bitcoin.
Step 1: Roll the dice 12 times.
7744 3664 8424 5514 3653 4582 1551 2812 5611 8325 6222 1414
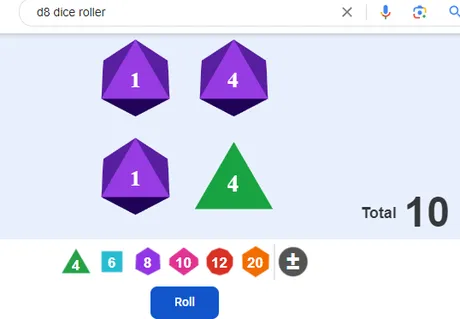
Notice anything?
If we had picked these numbers by hand instead of using dice we very likely would not have come up with a distribution like this. I max-rolled a 4 on the D4 die four times in a row at the start. That doesn't "feel" random but it absolutely is. Rolls like 1551, 5611, 6222, and 1414 also do not "feel" random. This is the problem with the human brain: we often see patterns where there are none.
A person would almost certainly not be able to create random numbers even if they appeared random to the naked eye. Again: entropy is a non-trivial task. Chaos theory is not simple. How many times would we personally randomly generate the 1111 roll? Probably never but it comes up just as often as all the other rolls when true-random is employed.
Step 2: Find the 12 words and note their binary form.
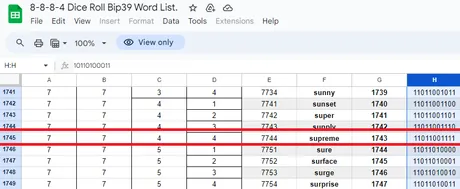
Scrolling down we see the first word is 'supreme'.
Ah what kismet serendipity.
The binary representation of this is shown to be 110 110 011 11. This translates to 6 6 3 3. So why 6633 instead of 7744 like we rolled? Because dice do not have a 0 roll, but binary, decimal, and hex can indeed be zero. Thus we must subtract one from the roll for a range of 0-7 on D8 and 0-3 on D4.
| Dice | Word | Binary |
|---|---|---|
| 7744 | supreme | 11011001111 |
| 3664 | finger | 01010110111 |
| 8424 | undo | 11101100111 |
| 5514 | motor | 10010000011 |
| 3653 | film | 01010110010 |
| 4582 | inhale | 01110011101 |
| 1551 | bamboo | 00010010000 |
| 2812 | destroy | 00111100001 |
| 5611 | neglect | 10010100000 |
| 8324 | trophy | 11101000111 |
| 6222 | pigeon | 10100100101 |
| 1414 | arrest | 00001100011 |
The last word is incorrect.
We must replace "arrest" by calculating the checksum, which is the hardest part. First, we must cut off the last 4 bits at the end (0011) to make room for the checksum.
| Dice | Word | Binary |
|---|---|---|
| 7744 | supreme | 11011001111 |
| 3664 | finger | 01010110111 |
| 8424 | undo | 11101100111 |
| 5514 | motor | 10010000011 |
| 3653 | film | 01010110010 |
| 4582 | inhale | 01110011101 |
| 1551 | bamboo | 00010010000 |
| 2812 | destroy | 00111100001 |
| 5611 | neglect | 10010100000 |
| 8324 | trophy | 11101000111 |
| 6222 | pigeon | 10100100101 |
| 1414 | ? | 0000110 |
Now we have exactly 128 bits of entropy which must be converted into hexadecimal.
11011001111010101101111110110011110010000011010101100100111001110100010010000001111000011001010000011101000111101001001010000110
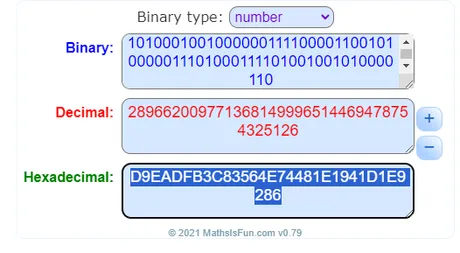
D9EADFB3C83564E74481E1941D1E9286
The checksum is then the first n / 32 bits of the SHA256 hash of the entropy.
Now we must run this hexadecimal number through SHA-256. However we have to make sure the tool we are using hashes hexadecimal, not unicode. Meaning that the hex can't be in a string format, otherwise we get the wrong answer.
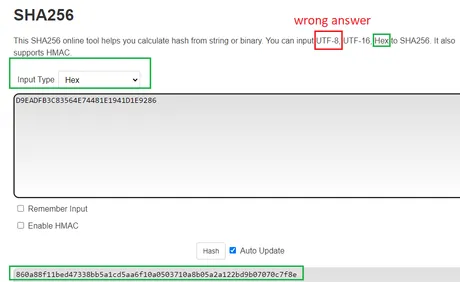
860a88f11bed47338bb5a1cd5aa6f10a0503710a8b05a2a122bd9b07070c7f8e
A 12-word seed is 128 bits. Divided by 32 is 4 bits for the checksum. A single hexadecimal character represents 4 bits, so the answer is just '8'. We only need the very first character of this hash (8). 8 in binary is represented by 1000 (2^3, with 2^0, 2^1, 2^2 being zero placeholders)

Finally!
So the checksum is 1000 and we can add it to the end of our last word.
| Dice | Word | Binary |
|---|---|---|
| 7744 | supreme | 11011001111 |
| 3664 | finger | 01010110111 |
| 8424 | undo | 11101100111 |
| 5514 | motor | 10010000011 |
| 3653 | film | 01010110010 |
| 4582 | inhale | 01110011101 |
| 1551 | bamboo | 00010010000 |
| 2812 | destroy | 00111100001 |
| 5611 | neglect | 10010100000 |
| 8324 | trophy | 11101000111 |
| 6222 | pigeon | 10100100101 |
| 1414 | ? | 00001101000 |
We can then search the BIP 39 spreadsheet for 00001101000.
And we find the magic word to be "artist".
Now we have a full 12 word key. Fully random to the best of our ability. Created 100% offline using dice and a computer with basic tools. Perhaps a Raspberry Pi Zero or at least one with no WIFI chip.
Now all that's left is to check our work.
EVM networks use this exact same protocol, so we can just plug it into Metamask and see if it works.
supreme finger undo motor film inhale bamboo destroy neglect trophy pigeon artist
And boom...

We get a fully secure random public EVM key of:
0x656b007Dba01B51C64BE974870Af9E6CD872A082
I verified this on both Metamask via Firefox browser and XDEFI wallet on Brave.
Both create the exact same public keys and associated private keys.
If we change the last word to "ask" the wallet throws an error because the checksum fails. However 1 out of 16 words will work (the ones that have a valid checksum). So words like "bachelor", "battle", and "beef" will work because the checksum is in alignment, but at the same time these words change the checksum from 1000 to 1001, 1010, and 0000 respectively. The hash makes it very difficult to guess which words will work and which will not without running the checksum math.
There are a total of 2048 words to choose from, so on average a 12-word seed will have 128 valid words that can fill the last slot while a 24-word seed would be limited to 8 words only out of the entire list. Therefore if anyone is looking for a more robust checksum due to potential user error a 24-word key would definitely be the way to go. Although I'm not sure how much that would help someone especially considering it means they have to keep track of 12 extra words with little to no added security.
What is the value of this?
Well theoretically we can use this knowledge to create private keys entirely offline. Dice rolls can be used for excellent random distributions, but also if we really wanted to we could choose our own words. However, I'm not quite sure how recommended that would be considering AI is becoming hyper advanced and might one day be able to hack the most popular word combinations.
Using word pairs like "battle dragon", "diamond hand", and "galaxy brain" could be a definitively bad idea over the long term, especially as crypto/AI becomes more popular. However they certainly would be much easier to remember, so one must weigh the risk of outside attack vs the risk of messing up and losing the keys via user error.
Even a hacked hardware wallet could be circumvented with this strategy
Imagine you get a hardware wallet in the mail that's designed to steal your crypto. How does it do this? Well it does all the things that the hardware wallet should do; it can't exfiltrate the keys, but what it can do is generate a pre-determined seed known to the attacker in advance. In such a situation creating your own keys offline would completely mitigate the attack and nothing would be lost. I have no idea how relevant that is to the real world, but somehow I feel like it's significant.
Conclusion
I've already spoken to this a couple times over in other posts, but the trust that we collectively put in the hands of companies like Trezor and Ledger is getting quite out of control. Ledger boasts that 20% of all cryptocurrency is stored on their devices, and they've just recently and purposefully added code that allows the device to exfiltrate the keys to 3 "trusted" parties for account recovery. This is a terrible risk and an obvious attack vector for three-letter agencies to exploit.
We need to figure out alternative ways to keep our keys completely offline and never expose any of this data to the Internet whatsoever. Being able to generate private keys with nothing but dice rolls and some basic algorithms could prove to be quite useful moving forward.
Crypto tells us to be our own bank. We wouldn't be doing our jobs if the size of our bags kept increasing but the level of security we employed stayed exactly the same no matter whether we held $10k or $10M. For now simply studying this type of entropy is good enough for me, but eventually someday down the line I'll be revisiting this exercise and creating a real offline key that I can actually use with confidence. It's only a matter of time before one of the major hardware wallet providers becomes compromised and catalyzes a bear market (2026? 2030? Ledger? Trezor?) and I'd rather not be too close to that explosion when it happens.
Return from Generating Entropy: Roll The Dice to edicted's Web3 Blog
