Automated market makers are the future of crypto.
They force everyone within the pools to buy and sell their assets at current market value. This creates exponential liquidity; the kind of liquidity that allowed me to purchase 1% of all LEO in existence the other day while barely moving up the price whatsoever. This is no joke, as trying to buy 1% of all BTC in existence would no doubt spike the price to absurd levels. On a percentage basis, AMM tokens have exponentially more liquidity than Bitcoin and other cryptocurrencies that don't have deep AMM liquidity pools. This allows new users to buy in at a good price without the token experiencing any kind of supply shock, granted liquidity providers do not remove their liquidity.

Why would LPs remove their tokens from the pool?
The better question is: why would LPs pool their tokens in the first place. The crux of AMM is yield. Without yield, it is impossible to make money within an LP pool. In fact, without yield, one is guaranteed to lose money within an LP.
What many users did not realize about AMM, especially in the early days of Uniswap, is that Impermanent Loss is a function of slippage. AMM is unique in that it forces not only the traders to accept slippage losses, but also the liquidity providers themselves. This is one of the things that makes it so easy to buy a ton of tokens without moving the price much. Because liquidity providers are accepting just as much slippage as the traders, the traders only feel the burden of slippage half as badly as they would otherwise.
Another thing that users realized during the early days of Uniswap is that the 0.3% exchange fee that goes to LPs is not nearly enough during extreme bull markets when traders are pouring money into these next-gen tokens. The impermanent losses then become permanent because the price of the token never dips back down to the low levels it was at before. This in turn created a reactionary development fork whereby many of the new AMM exchanges are trying to mitigate the "damages" of impermeant losses; something which I explained in my last post is a mistake. All that is needed to curb IL is higher yield. This can be accomplished by printing more inflation or simply allowing LPs to exit the pool as the risks become too extreme.
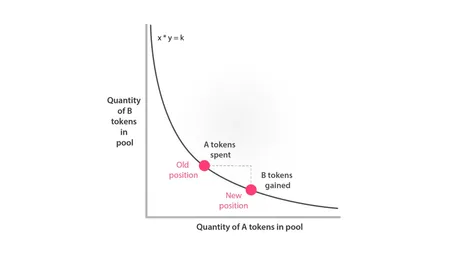
The main topic I'd like to go over in this post is the equation of the simplest form of AMM: x*y=k. This equation is a deceptively simple yet effective means of providing infinite liquidity to these emergent markets. By using this logarithmic curve it is impossible to run out of tokens in one direction or the other. Rather, the prices of the tokens changes as the ratio within the pool fluctuates. I will more accurately explain how this works now.
This is the more complicated version of y*x=k.
It took me about an hour of research before I realized how this actually works. This topic is explained extremely poorly across the vast majority of tutorial websites. Chalk that up to computer scientists not being good teachers.
Step one: calculate constant k.
Once we know the value of the constant k the equation becomes possible to solve. What a lot of these websites don't actually tell you is how easy it is to solve for k. The equation above shows R(alpha) minus delta alpha times R(beta) plus delta(beta) equal to k. delta(beta) is also being multiplied by an exchange fee gamma. Let me tell you: that's way more complicated than it needs to be.
k is easily calculated by reducing delta to zero.
Assuming no trade is taking place, there is no delta, and there is no fee. This simplifies the above equation down to the simple k=y*x form, where x and y are just the amount of tokens in the pool.
example
Say the internal market on Hive (Hive/HBD) was converted to AMM from the currently outdated orderbook. With a current price of $1.70 it's safe to assume that the ratio of Hive to HBD would be 1:1.7. For every one Hive there would be 1.7 HBD inside the pool, validating the current price.
Calculating how much hive/HBD comes out of the pool depends on how much slippage occurs when traders pump one side and extract tokens out the other. For simplicity, lets say there are 10M Hive tokens in the pool and 17M HBD tokens, for a total value of $34M locked in the LP.
So what happens if we dump 20,000 HBD into this pool?
k = x * y, where x and y are Hive/HBD. Therefore, k = 10M * 17M = 170,000,000,000,000 170 trillion is the constant.
How much Hive will be extracted?
We now know the following variables:
- k = 170,000,000,000,000
- R(alpha) = 10,000,000 Hive
- R(beta) = 17,000,000 HBD
- delta(beta) = 20,000 HBD pumped in
- delta(alpha) = ??? Hive extracted out
Now we just have to solve for x.
You'll also noticed I'm ignoring the fee (gamma). The fee is an unnecessary complexity (another tidbit that the tutorial websites fail to mention). In fact, we can calculate the fee before or after the transaction takes place, making it completely irrelevant to the equation itself.
For example, we can calculate the fee in terms of HBD before the transaction goes through. Assuming a 0.1% fee, this would mean a 20 HBD fee would be taken before the equation even needs to be solved. Therefore we'd just modify delta(beta) to 19,980 HBD, handling the fee before solving for x in the first place. The 20 HBD would then simply be added to the LP pool and given to liquidity providers or used for another purpose entirely.
It's also possible to calculate the fee after we solve for x. This would charge the fee in terms of Hive instead of HBD. It's significant to note that charging the fee after the equation is solved means that the fee is slightly lower than it would be if it was calculated beforehand. This is because every trade as some amount of slippage, so the higher the slippage involved, the bigger the discount the trader can get on the fee if it is calculated beforehand (because the slippage is removed before the fee is taken into consideration). However, this difference in value is usually extremely insignificant in the grand scheme of things (unless we were creating a reflection token with an extremely high fee).

Solving for x
(10,000,000 Hive - x Hive)(17,000,000 HBD + 20,000 HBD) = 170T (170,000,000,000,000 / 17,020,000) = 9,988,249.1186839 10,000,000 - 9,988,249.1186839 - = 11,750.881316
Therefore 20k HBD got us 11,750.8813 Hive.
We were able to buy Hive for $1.702. Which is obviously very good slippage compared to the $1.70 listing. Of course this is before any fee is applied (if any).
A 0.1% fee applied to the 11,750.8813 Hive would be 11.75 Hive. Which ends up pretty much being exactly $20 because the price of Hive has increased slightly (unless arbitrage from exchanges comes into play). At best this trader could have saved like 3 cents from the fee be calculated after the fact. Again, calculating the fee before or after the solve is largely irrelevant and does not come into play during the solve (something the tutorial websites once again do not clarify well).
To Recap:
Calculating the AMM function becomes very easy once you've tried it a few times.
-
k = x * y
- Calculate k by multiplying the total number of tokens within both sides of the pool together.
- Add the amount of tokens being pumped into one side.
- Divide k by the new number of tokens in the pool k/(y+dy).
- Subtract k/y by the old x value to determine how many tokens were taken from the pool and given to the buyer.
- Calculate the fee before or after the trade is done and don't include this number when solving for x/y.
The 'simplified' formula:
dx = x - k/(y+dy)
11,750.8813 = 10,000,000 - (170,000,000,000,000 / 17,020,000)
Deceptively simple.
Like crypto itself, this process is extremely simple once we figure it out and extremely complicated before we realize what exactly is going on here. Many DEX protocols are coming up and more and more complex equations to do things like mitigate impermanent losses and the like, but I think the simplest way is the best way. There is no reason to mitigate losses when the reward for providing liquidity is so high in the first place.
But wait, there's more!
Because after 11,750.88 Hive gets extracted from the pool, well then we have to calculate the constant k all over again. Actually you don't have to if you don't charge a fee. k only changes when the number of LP tokens changes.
9988249.1186839012925969447708578 * 17,020,000 = 170T
The biggest changes in k happen when users add or subtract liquidity to the pool, and it changes ever so slightly if the exchange fee is given to the liquidity providers. The higher the constant, the more liquidity the pool has and the better off everyone will be in terms of slippage and impermeant losses. However, the higher the value of k the more competition there is in the pool and less yield will be allocated per LP token. More liquidity means less yield for everyone, but also less risk of IL and slippage. Double edged sword.
We also have to calculate the new value of Hive.
For example, how much HBD would we have to pump in to make Hive do an x4? Rather than a 1:1.7 ratio we'd need a 1:6.8 ratio. This is accomplished by doubling the amount of HBD in the pool (17M to 34M) while extracting half of the Hive (5M) for a new ratio of 5M Hive to 34M HBD and a new price of Hive at $6.80 (assuming HBD is still worth $1).
Aftermath... get it? After... math... kek.
So we did it! We pumped in 20k HBD on one side and we extracted about 11,751 Hive from the pool. However, this isn't quite the end of our little adventure. What if the AMM pool on Hive didn't have that much liquidity? What if there were only 1M Hive tokens and 1.7M HBD? In this case we would have only extracted 11,628 Hive instead of 11,751 due to less liquidity and higher slippage. Still, we see that AMM provides exponential liquidity and even in this case with x10 less LP provided we only lost a couple hundred bucks on the $20000 trade. Not too shabby.
It's also important to note that this LP pool would have exactly as much liquidity as Hive wanted it too. Meaning all that matters is how much inflation/yield we allocate to the pool. Allocating high inflation would ensure that liquidity would be quite high, while allocating low inflation would ensure that money wasn't being wasted and diluted for no reason. These are things that the network must figure out the best recipe for success. In my opinion high liquidity and high inflation is absolutely necessary going forward, but even a tiny bit of yield applied to the internal market would be a vast improvement when compared to archaic orderbooks.
It is in this way that Hive will finally have an actual stable coin that works. HBD will never be able to hold its peg without this kind of exponential liquidity that AMM provides. All in good time I suppose, there are a lot of priorities when it comes to Hive, and we are progressing quite quickly on several fronts at once. HAF and RC-pools are quite a strong focus at the moment. Still it's good to be mindful of this potential upgrade to the internal market because I believe it's something that could easily 10x the value of Hive upon successful implementation (especially depending on the depth of the liquidity incentivized by high yield).
Wait, 10x? How?
Well, imagine we are allocating massive yield to this AMM farm. This incentivizes users to power down and buy coins off exchanges to enter the pool. Not only that, for every Hive that enters the pool, it must be matched by an equal amount of HBD. Imagine we were providing so much yield to this AMM that we needed 100M HBD just to satisfy the demand to participate.
Where does that 100M HBD come from? It currently doesn't exist, and a massive amount of Hive would get burned to mint it. Once again, all these factors push up the price. On top of this fact less Hive would be powered up, which means there's less competition in the blogger reward pool. Transitioning the internal market to an AMM not only jacks up the price of Hive, but it also makes all upvotes on the blogging side of things bigger as well (in terms of Hive and even more in terms of USD). It does all these things AND it stabilizes the price of HBD. It's really the obvious play at this point.
The answer is simple: an AMM internal market would easily x10 the value of Hive given enough yield to incentivize it. Yeah, you heard me right: printing money creates value. Stop listening to deflationary maximalists. Those guys are delusional. Inflation that gets printed can EASILY generate more value than it dilutes, and AMM technology and infinite liquidity provision is a primary example of such developments. Hive could double its emission rate while x10ing the spot price. It's the best of both worlds really.
Conclusion
Well this post actually was a lot longer than I wanted it to be. I was hoping to just have a bare-bones tutorial about how the AMM function works. Better luck next time I suppose.
AMM is the future of crypto. There really is no other option. AMM is a technology that has been around for a very long time, but only just recently was crypto able to provide the necessary yield required for deep liquidity pools that allocate massive rewards to those willing to risk impermanent losses. I guess that's the advantage of being your own central bank: all of a sudden tools that made no sense become the superior option.
x*y=k. Don't let the fee complicate the issue.
Providing infinite liquid markets has never been easier.
Posted Using LeoFinance Beta
Return from k = x * y : AMM equation explained to edicted's Web3 Blog
